Le produit vecteur d’OSO 2017 est enfin sorti ! Après plusieurs semaines de traitements, les vecteurs de chaque département sont disponibles ici. La production requiert la mobilisation d’une grande quantité de ressources de calcul et une stratégie de traitements un peu particulière. Nous voulions vous expliquer comment parvient-on à produire cette couche d’information.
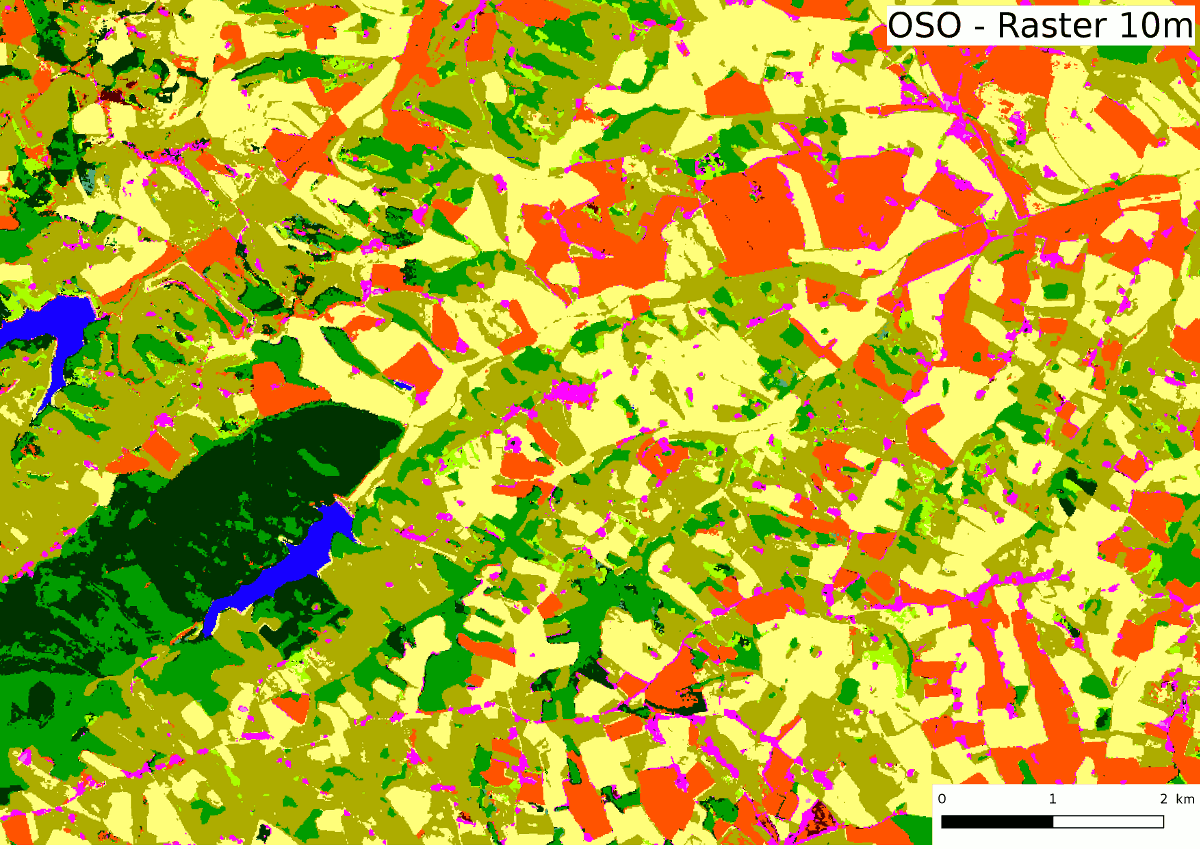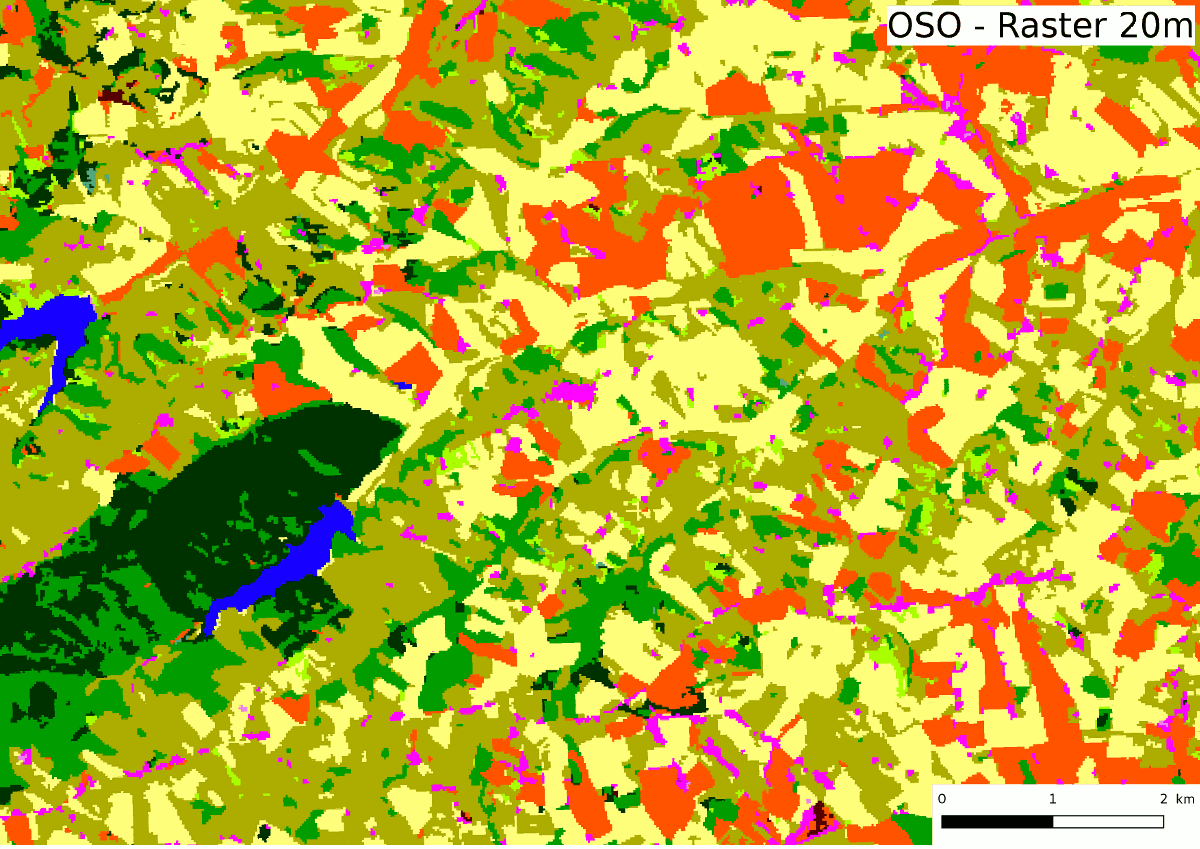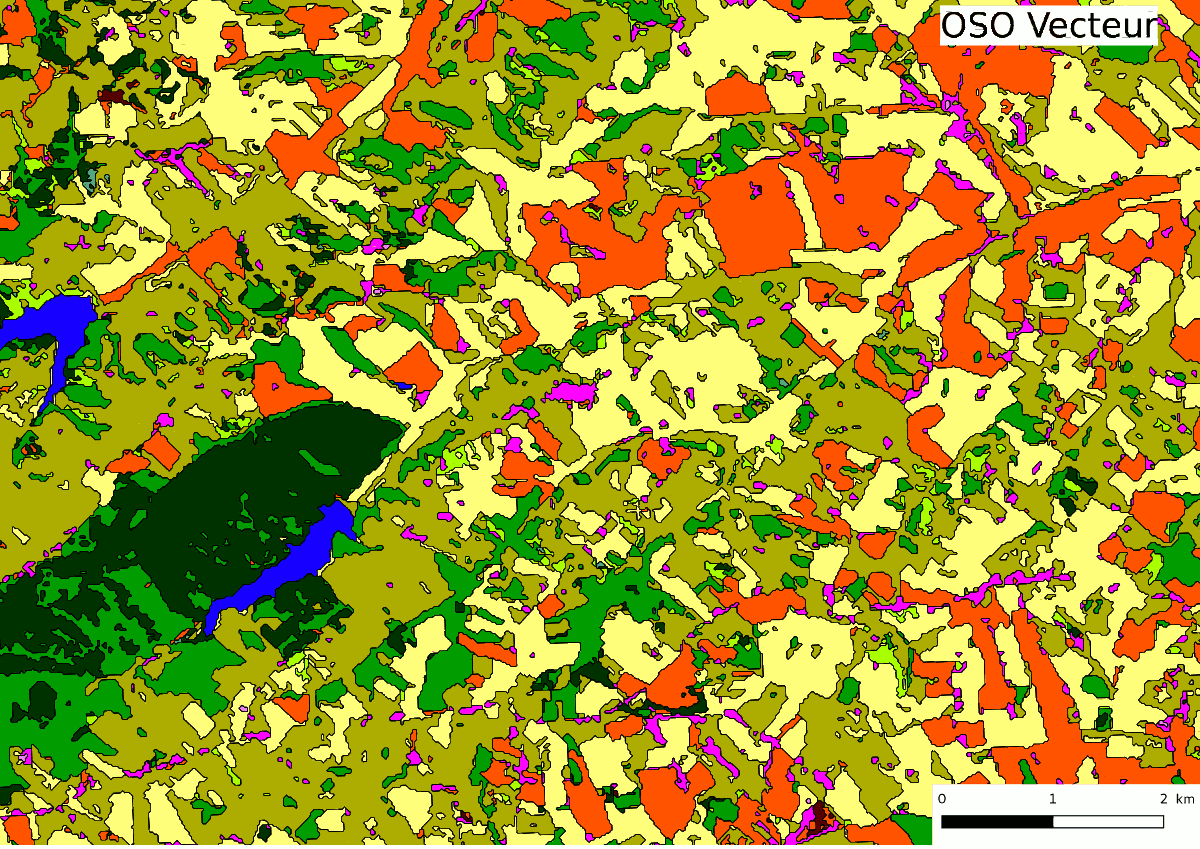
A priori, le plus simple serait de prendre la couche raster issue de la chaine de traitements iota² de l’intégrer dans notre logiciel SIG préféré et d’appuyer sur le bouton « Vectorisation » ! Mais les choses ne sont pas si simples, certaines contraintes et besoins nous obligent à quelques tours de passe-passe :
- Tout d’abord, comment vectoriser un raster de plus 15 milliards de pixels sans dépassement mémoire ?
- Le crénelage issu de la couche raster ne plait pas à la plupart des utilisateurs. un produit simplifié et lissé serait plus approprié.
- Et comment s’assurer de la pertinence topologique des produits vectoriels obtenus ?
Un format vectoriel topologique
Il s’agissait, dans un premier temps, d’identifier un format vectoriel basé sur le modèle « topologique » (à la différence du modèle « spaghetti »). Le modèle « topolgique » considère une couche vectorielle comme un graphe d’arcs connectés et non d’entités indépendantes. Ce graphe recense l’ensemble des relations de voisinage et d’appartenance de chaque élément géographique (noeud, arc, polygone) de la couche. Dans ce contexte, toute déformation d’une couche vectorielle basée sur ce modèle ne modifie pas les relations d’adjacence. En d’autres termes, en déformant des polygones, par exemple en éliminant des noeuds pour les simplifier, aucun trou entre polygone est généré, à la différence d’un modèle spaghetti.
Il existe plusieurs formats « topologiques ». Nous en citerons 2 :
- TopoJSON qui est une extension topologique du format GeoJSON. Il est adapté à la publication cartographique en ligne.
- Le format vectoriel de la bibliothèque Grass
Après quelques expérimentations, il s’est avéré que la bibliothèque vectorielle Grass était la plus adaptée à nos besoins, en partie pour ses possibilités de lissage non disponibles avec la librairie TopoJSON ainsi qu’un ensemble de fonctions vectorielles de base nécessaire à nos traitements.
Afin de limiter la charge mémoire nécessaire à la vectorisation d’un raster deplus de 15 milliards de pixels, nous avons eu recours à 2 solutions :
- effectuer la vectorisation sur un produit régularisé à 20 m issu du produit initial à 10 m,
- sérialiser / paralléliser les traitements de vectorisation.
La régularisation
La phase de régularisation a consisté à appliquer plusieurs filtres majoritaires successifs pour gommer les pixels isolés, grâce à l’outil gdal_sieve. Afin d’assurer une cohérence sémantique, des règles « métier » de régularisation ont été appliquées. Par exemple, des pixels isolés (a priori un seul pixel) de cultures annuelles (cultures d’été ou d’hiver) peuvent être remplacés uniquement par des pixels de ce même groupe. Dans la même philosophie, des pixels de feuillus ne peuvent être remplacés que par des pixels de résineux. A l’issue de cette étape, le raster d’occupation du sol à 20 m de résolution spatiale ne possède plus que 2.8 milliards de pixels.
La couronne d’adjacence
Nous avons donc développé une méthode de parallélisation et de sérialisation des traitements. La difficulté méthodologique concerne la dépendance spatiale et sémantique des polygones ou des entités (agrégats homogènes de pixels ou clump). Il est impossible de découper la donnée géographique en zones homogènes régulières (tuile) indépendantes. Une entité doit être traitée dans son ensemble. Dans le cas d’une simple vectorisation, le traitement parallèle de sous-ensemble d’entités de pixels est réalisable. Cependant, dans le cas d’une opération de simplification (modification topologique), il est nécessaire de prendre en compte le voisinage des entités / polygones à simplifier, pour ne pas perdre la cohérence topologique (trous, biais de simplification) au moment de la fusion des sous-ensembles. Une couronne d’adjacence autour des entités / polygones à simplifier est donc calculée et associée à chaque traitement parallèle. Ainsi, un même polygone est impliqué dans au moins deux traitements de simplification, en tant qu’entité à simplifier et en tant qu’élément de la couronne d’adjacence. De cette façon, les sous-ensembles de polygones simplifiés peuvent être assemblés à l’échelle géographique souhaitée sans risque d’incohérence topologique.
Le principe méthodologique de cette approche est illustré grâce à la carte ci-dessous. Le territoire est découpé en tuiles.

Pour la vectorisation de la France, nous nous appuyons sur un ensemble de 100 tuiles, ce nombre de tuiles est un peu arbitraire. Chaque tuile est traitée en parallèle (indépendance sémantique et topologique). Au sein d’une tuile, les entités (agrégats) de pixels de la tuile sont extraits ainsi que les entités de la couronne d’adjacence. Cette opération, bien que relativement simple, est très couteuse en ressources (RAM, processeurs et temps de traitement). Les applications OTB utilisées pour réaliser cette opération sont :
La vectorisation
A l’issue de cette opération, la plus lourde du traitement de vectorisation, un raster localisant les entités et sa couronne d’adjacence est disponible pour chaque tuile. La seconde phase de traitements peut commencer. Pour chaque département (produits en parallèle), les rasters des tuiles intersectant le département sont mosaïquées. Ce raster d’occupation du sol mosaïqué peut finalement être :
- vectorisé,
- simplifié avec l’algorithme de Douglas-Peucker 1,
- lissé avec des splines cubiques d’Hermite 2,
- filtré en supprimant les polygones dont la superficie est inférieure à l’unité minimale de collecte / cartographique et
- découpé à l’échelle du département !

Dans l’intérêt de préserver au mieux les informations d’occupation du sol initiales, à savoir celles produites par iota², un calcul de statistiques zonales est effectué. Cette opération, bien qu’assez simple est elle aussi gourmande en ressources, puisqu’il s’agit de compter pour chaque polygone le nombre de pixels initiaux de chaque classe d’occupation du sol OSO. Il existe plusieurs méthodes (par exemple en utilisant les applications otbcli_SampleSelection et otbcli_SampleExtraction de l’OTB), nous avons opté pour l’outil gdalwarp et la librairie scikit-image pour parvenir à cette information qui consiste à comparer une donnée vectorielle avec une donnée raster.
Finalement, une des difficultés de cette opération de production réside dans l’attribution des ressources de calcul pour la phase de détection de la couronne d’adjacence. Elles sont en effet entièrement dépendantes de la continuité paysagère de la couronne d’adjacence de la tuile traitée. Comme le montre la figure ci-dessous, les emprises de ces couronnes adjacence sont très variables.

Quelles ressources ?
Pour produire la vectorisation de la France, nous avons eu besoin de quelques ressources informatiques et d’un peu de temps, comme l’atteste le tableau ci-dessous :
| Régularisation | ||||
| Calcul des entités raster | ||||
| Couronnes d’adjacence | ||||
| Vectorisation | ||||
| Statistiques zonales | ||||
| Jointure |
Quelques statistiques pour finir…
On obtient un total de 12.7 millions de polygones sur l’ensemble de la France métropolitaine (continent plus Corse). Le plus grand a une taille de 350 000 ha et se trouve en Gironde, je vous laisse deviner de quel élément paysager il s’agit ?!
Et le code, pour aller plus loin !
L’ensemble des traitements présentés ci-dessus sont disponibles sur le dépôt git de iota² : https://framagit.org/inglada/iota2/tree/master/scripts/simplification. N’hésitez pas à nous faire des retours, des propositions d’amélioration ou des critiques !
Bibliographie
1. David H Douglas et Thomas K. Peucker, « Algorithms for the reduction of the number of points required to represent a digitized line or its caricature », Cartographica: The International Journal for Geographic Information and Geovisualization, University of Toronto Press, vol. 10, no 2, 1973, p. 112-122 ↩2. Bartels, R. H.; Beatty, J. C.; and Barsky, B. A. « Hermite and Cubic Spline Interpolation. » Ch. 3 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann, pp. 9-17, 1998. ↩

Bonjour Vincent,je viens de charger la version OSO 2017 pour le département et il me semble qu’il y a un gros bug : j’ai 597 ha d’urbain dense et 23485 ha d’urbain diffus ! En regardant de près ce n’est pas une inversion mais je pense que les lottissements ont été classés en diffus. Par exmple, St Cyprien et Argelès sont presque totalement en diffus. Et c’est pareil pour tous les villages de Cerdagne.Amitiés,Jacques
Bonjour Vincent,j’ai regardé le produit raster, qui lui me semble correct, finalement je pense qu’il s’agit d’une inversion dans la nomenclature entre raster et vecteur.AmitiésJacques FERAUD
Bonjour Jacques,Après vérification, il s’agit seulement d’une inversion de couleurs au niveau de l’interface de visualisation du produit raster. Tout devrait rentrer dans l’ordre. Merci de ton œil avisé.Bien à toiVincent
« prendre la couche raster issue de la chaine de traitements , l’intégrer dans notre logiciel SIG préféré et d’appuyer sur le bouton « Vectorisation » ! « c’est exactement ce que j’avais fait en 2013 avec les données de submersion marine issues de Litto3D (MNT IGN/SHOM à 1 m de résolution en xy et 20 cm en z, donc quelques milliards de pixels aussi) et c’est vrai que le résultat (de gdal_polygonize) est globalement inutilisable dans un SIG.Vos explications lumineuses me font comprendre qu’il est temps de reprendre tout ça, merci, notamment pour l’idée d’utiliser le format topologique de Grass.