![]() Attention, cet article contient des formules.
Attention, cet article contient des formules.
Les effets du reliefs sont un des éléments perturbateurs de la mesure de réflectance de surface. Il est facile de s’en rendre compte sur l’image ci-dessous des pyramides de Gizeh.

Les effets du relief sur les réflectances observées proviennent de plusieurs phénomènes, schématisés dans l’illustration ci-dessous.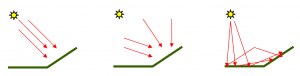
- plus la surface est perpendiculaire à la direction solaire, plus elle va recevoir d’énergie par unité de surface (on parle d’éclairement). Si la surface est parallèle à la direction solaire, elle ne reçoit pas de lumière directe du soleil, l’éclairement direct reçu est donc nul.
- Pour une surface horizontale : \( E_h= E_0.T_{dir}^\downarrow.cos(\theta_s) \)

Définition de l’angle zenithal solaire et de l’angle d’incidence
- Pour une surface inclinée \( E_i=E_0.T_{dir}^\downarrow.cos(\theta_i) \)
- \( E_0 \) est l’éclairement solaire en haut de l’atmosphère, et \( T_{dir}^\downarrow \) est la transmission directe descendante, c’est à dire la proportion de cet éclairement qui rejoint directement la surface sans être diffusé par l’atmosphère.
- Si on suppose que tout l’éclairement est direct, la réflectance mesurée si la surface avait été horizontale se calcule à partir de la formule suivante : \( \rho_h=\rho_i \frac{cos(\theta_s)}{cos(\theta_i)}\). Cette formulation a tendance à surcorriger l’effet des pentes.
- Pour une surface horizontale : \( E_h= E_0.T_{dir}^\downarrow.cos(\theta_s) \)
- Les surfaces reçoivent aussi un éclairement solaire diffusé par l’atmosphère. Si la surface n’est pas horizontale, une partie du ciel est masquée par la pente: l’éclairement diffusé par l’atmosphère et qui parvient à la surface est donc réduit. Cet éclairement va varier en fonction de la quantité d’aérosols (et de nuages) présents dans l’atmosphère. Par ailleurs, les reliefs environnants peuvent aussi masquer une partie du ciel, mais nous ne prenons pas cet effet là en compte dans notre modélisation. Nous utilisons l’approximation suivante, qui revient à supposer que la pente est le seul endroit incliné dans un environnement horizontal.
- Si la surface est horizontale, la fraction de ciel Fciel vue est 1, si la surface est verticale, la fraction de ciel vue est 1/2
- \( \displaystyle Fciel= \frac{1+cos(pente)}{2} \)
- enfin, la pente peut recevoir de la lumière des surfaces environnantes, qui deviennent directement visibles. Dans notre modélisation simplifiée, nous supposons toujours que tout l’environnement de notre pente est plat et nous ne prenons pas en compte l’effet du versant opposé dans une vallée.
- Si la surface est horizontale, la fraction de sol vue est 0, si la surface est verticale, la fraction de sol vue est 1/2.
- \( \displaystyle Fsol= \frac{1-cos(pente)}{2} \)
Au final, pour calculer la réflectance mesurée si la surface avait été horizontale \( \rho_{h}\), en fonction de la réflectance mesurée sur la surface inclinée \( \rho_{i}\), on obtient donc la formule suivante :
\( \rho_{h}=\displaystyle \rho_{i}.\frac{T^{\downarrow}}{T_{dir}^{\downarrow}.\frac{cos(\theta_i)}{cos(\theta_s)} + T_{dif}^{\downarrow} F_{ciel} + T^{\downarrow} F_{sol} \rho_{env}} \)
où \( T^{\downarrow}\) est la transmission descendante composée d’une partie directe et diffuse : \( T^{\downarrow}= T_{dir}^{\downarrow}+ T_{dif}^{\downarrow}\), et [/latex]\rho_{env}[/latex] est la réflectance moyenne autour du pixel à corriger. Enfin, on peut aussi prendre en compte un facteur de correction lié aux effets directionnels, mais cet aspect est délicat, car les effets directionnels varient en fonction du type de surface observé. Voir par exemple : Dymond, J.R.; Shepherd, J.D. 1999: Correction of the topographic effect in remote sensing. IEEE Trans. Geosci. Remote Sens. 37(5): 2618-2620. Il est très difficile de valider cette correction : pour bien le faire, il faudrait comparer des images acquises à différentes heures de la journée. Malheureusement, tous les satellites à haute résolution passent à peu près à la même heure. On peut essayer cependant de vérifier que des surfaces ayant un couvert semblable (une prairie, une forêt) sur des versants opposés, présentent bien la même réflectance après correction. Les points les plus propices à ce genre de vérifications sont des vallées Nord Sud. Voici quelques exemples de résultats après correction.

Enfin, un élément essentiel de la précision de cette méthode est la disponibilité d’un modèle numérique de terrain très précis, pour le moment, le seul MNT disponible globalement est SRTM à 90 mètres de résolution. Sa précision est un peu insuffisante et laisse parfois des artefacts, si les ruptures de pentes sont mal localisées.

A l’échelle globale, il existe également le produit ASTER Global Digital Elevation Map (http://asterweb.jpl.nasa.gov/gdem.asp) de meilleure résolution spatiale (30 m) que le SRTM mais souffrant de nombreux artefacts et imprécisions. Généralement le SRTM est préféré.Damien J.
Et comment connaître ρ_env avant la correction ? par itération ?
Merci pour cette question. Nous calculons simplement la moyenne des réflectances sur un voisinage de deux kilomètres sur les données de réflectance de surface avant correction des effets d’environnement et des effets de pente, en espérant que tous les effets se compensent et donc que cette moyenne ressemble à celle qu’on aurait après correction. Une démarche itérative serait possible et améliorerait la qualité du résultat, mais elle ne me parait pas envisageable sur une chaîne qui doit pouvoir traiter le monde entier avec Sentinel-2 et doit donc tourner vite.