![]() Attention, cet article contient beaucoup de formules.
Attention, cet article contient beaucoup de formules.
Les grandeurs radiométriques sont nombreuses et au premier abord, il n’est pas facile de s’y retrouver. Voici un petit guide des différentes grandeurs que rencontrera tout utilisateur de données de télédétection. C’est un peu rébarbatif, et c’est bourré de formules compliquées, avec des intégrales et tout 😉 , mais bon, il faut en passer par là pour bien comprendre nos images. Allez courage !
Radiométrie
Les détecteurs des instruments optiques sont sensibles à l’énergie lumineuse qu’ils reçoivent pendant un temps d’observation. Sur un appareil photo, ce temps de pose correspond à l’intervalle entre l’ouverture et la fermeture de l’obturateur. Sur un instrument d’observation numérique, on utilise davantage le terme “temps d’intégration” : celui-ci est souvent fixé par l’électronique de l’instrument. L’énergie reçue est reliée aux propriétés de la scène observée, mais dépend aussi de nombreux autres paramètres liés à l’instrument lui même, ce qui n’est pas pratique lorsqu’on cherche, par exemple, à comparer des mesures prises par des instruments différents. Nous allons définir successivement, dans les paragraphes qui viennent, des grandeurs physiques qui permettent peu à peu de s’affranchir de ces paramètres dépendant de l’instrument pour obtenir une caractéristique de la surface observée seulement. Ceci va nécessiter de définir toute une série de grandeurs physiques : la description de cette série de grandeurs peut être ressentie comme rébarbative par les étudiants (et même par leur professeurs…), mais s’avère finalement bien utile un jour ou l’autre pour comprendre ce qui est observé.
Energie, Energie spectrale, Sensibilité spectrale, Energie Equivalente
Un détecteur est sensible à une énergie ε, exprimée en joules (j), reçue au cours du temps d’intégration t i. Cette énergie est apportée par des photons de différentes longueurs d’onde. En fonction de la scène observée, l’énergie spectrale ε(λ) reçue dans chaque longueur d’onde varie. L’énergie spectrale est exprimée en joules par unité de longueur d’onde (souvent en j/µm). Il faut, de plus, tenir compte du fait que l’instrument présente une sensibilité spectrale différente S(λ) en fonction des longueurs d’ondes. S(λ) est une grandeur sans unité.

L’énergie reçue pendant le temps d’intégration par un instrument dont la sensibilité est non nulle dans l’intervalle de longueurs d’onde [λ1, λ2] s’exprime donc de la manière suivante :
$$\epsilon=\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\epsilon(\lambda)\, d\lambda$$
Pour un instrument donné, plus la bande spectrale [λ1, λ2] est large, plus l’énergie collectée va être grande. Pour éviter de devoir manipuler des intégrales dans les formules, il est utile de définir l’énergie spectrale équivalente comme la moyenne de l’énergie spectrale dans la bande [λ1, λ2], pondérée par la sensibilité spectrale.
$$\epsilon_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\epsilon(\lambda)\, d\lambda}{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda}$$
L’avantage de cette unité est que l’énergie spectrale équivalente ne dépend plus de la largeur de bande si l’énergie spectrale ne varie pas dans la bande.
Le flux
Pour une longueur d’onde donnée, l’énergie spectrale est l’intégrale de la puissance lumineuse qui parvient sur le détecteur pendant le temps d’intégration, cette puissance lumineuse est appelée le Flux Spectral et s’exprime en Watts par unité de longueur d’onde (souvent en W/µm).
$$\phi(\lambda)=\frac{d\epsilon(\lambda)}{dt}$$
On peut, comme pour l’énergie, définir le flux spectral équivalent, de la manière suivante :
$$\phi_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\phi(\lambda)\, d\lambda}{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda}$$
et il suffit de développer cette formule pour vérifier que les grandeurs équivalentes sont reliées de la même manière que les grandeurs spectrales :
$$\phi_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{d\epsilon_{eq\,[\lambda_{1},\lambda_{2}]}}{dt}\label{eq:flux-energie-equivalente}$$
Le flux qui parvient à l’instrument reste cependant une grandeur bien éloignée des propriétés optiques de la scène que nous cherchons à mesurer. Il dépend par exemple de la surface du détecteur. Pour s’affranchir de ce paramètre, il est nécessaire d’introduire une nouvelle grandeur : l’éclairement.
L’éclairement
L’éclairement (spectral) est le flux (spectral) qui parvient au détecteur par unité de surface ds du détecteur, il se définit donc par :
$$E(\lambda)=\frac{d\phi(\lambda)}{ds}$$
De même, l’éclairement solaire équivalent se définit par :
$$E_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)E(\lambda)\, d\lambda}{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda}=\frac{d\phi_{eq\,[\lambda_{1},\lambda_{2}]}}{ds}$$
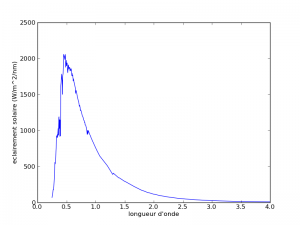
L’éclairement permet par exemple de caractériser la puissance lumineuse qui parvient sur une surface perpendiculaire à la source lumineuse, par unité de surface. L’éclairement solaire reçu sur terre varie avec la distance terre soleil, qui varie au cours de l’année. L’éclairement solaire intégré au jour j pour une surface perpendiculaire au soleil vaut$$E(j)=E_{0}\frac{d^{2}(j)}{d_{0}^{^{2}}}$$, avec E0 = 1367 w / m2 et $$\frac{d^{2}(j)}{d_{0}^{2}}=(1-0.01673*cos(2\pi/365.3*(j-j0-2)))$$, et j0 est le 01/01/1950. L’éclairement solaire spectral présente de fortes variations avec la longueur d’onde.
L’éclairement est une grandeur bien utile, mais qui dépend quand même du champ de vue du détecteur. Plus celui-ci sera réduit, plus l’éclairement sera réduit. Il dépend également de l’orientation du détecteur par rapport à la direction d’où provient la lumière. Par exemple, si le détecteur est orienté parallèlement à la direction des photons, il ne recevra pas de lumière. Inversement, lorsque le détecteur est perpendiculaire à la direction lumineuse, il reçoit un éclairement maximal. Pour obtenir une unité indépendante des caractéristiques de l’instrument, nous allons donc devoir définir une nouvelle grandeur (oui, encore une…).
La Luminance
La Luminance spectrale est le flux spectral qui parvient à l’instrument par unité de surface ds et par unité d’angle solide dΩ, et ce perpendiculairement à la surface du détecteur.
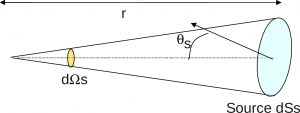 Définition de l’angle solide $$d\Omega_{s}=\frac{dS_{s}cos\theta_{s}}{r^{2}}$$. L’angle solide s’exprime en stéradians (sr)La luminance s’exprime en w / m2 / sr
Définition de l’angle solide $$d\Omega_{s}=\frac{dS_{s}cos\theta_{s}}{r^{2}}$$. L’angle solide s’exprime en stéradians (sr)La luminance s’exprime en w / m2 / sr
$$L(\lambda)=\frac{d^{2}\phi(\lambda)}{ds\, d\Omega\, cos\,\Theta_{s}}$$
La grandeur d2G = ds. dΩ . cos Θ s est très utilisée par les opticiens et s’appelle l’étendue géométrique. Le flux spectral obtenu en entrée d’un instrument de surface S et dont le champ couvre l’angle solide Ω s’écrit donc :
$$\phi(\lambda)=\intop_{S}\intop_{\Omega}L(\lambda)cos\,\Theta_{s}ds\, d\Omega\,=\iint_{G}L(\lambda)d^{2}G$$
Comme pour les autres grandeurs, on définit la luminance spectrale équivalente de la manière suivante :
$$L_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)E(\lambda)\, d\lambda}{\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda}=\frac{d^{2}\phi_{eq\,[\lambda_{1},\lambda_{2}]}}{ds.d\Omega.cos\,\Theta_{s}}=\frac{d^{2}\phi_{eq\,[\lambda_{1},\lambda_{2}]}}{d^{2}G}$$
Lorsque l’étendue géométrique est petite, ce qui est en général le cas en télédétection, on peut écrire :
$$L_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{\phi_{eq\,[\lambda_{1},\lambda_{2}]}}{G}\label{eq:flux-luminance-=0000E9tendue}$$
La luminance (dont l’unité est le W.m-2.sr-1) est une grandeur très utilisée en télédétection, puisqu’elle combine plusieurs avantages :
- l’énergie mesurée par un détecteur est proportionnelle à la luminance équivalente. En effet, pour un instrument d’étendue géométrique G, de sensibilité spectrale S(λ) dans la bande [λ1, λ2], qui effectue des mesures pendant le temps d’intégration ti, la mesure X obtenue par le détecteur de l’instrument s’exprime de la manière suivante :
$$X=\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\epsilon(\lambda)\, d\lambda=\left(\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda\right).\epsilon_{eq\,[\lambda_{1},\lambda_{2}]}.$$
Et en utilisant les formules [eq:flux-energie-equivalente] et [eq:flux-luminance-=0000E9tendue], on obtient donc
$$X=\left(\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda\right).\phi_{eq\,[\lambda_{1},\lambda_{2}]}.t_{i}=\left(\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda\right).L_{eq\,[\lambda_{1},\lambda_{2}]}.G.t_{i}=S{}_{[\lambda_{1},\lambda_{2}]}.L_{eq\,[\lambda_{1},\lambda_{2}]}.G.t_{i}$$
avec $$S_{_{[\lambda_{1},\lambda_{2}]}}=\intop_{\lambda_{1}}^{\lambda_{2}}S(\lambda)\, d\lambda$$, sensibilité du détecteur dans la bande [λ1, λ2].
Ce qui revient donc à écrire que :
$$X=A.L_{eq\,[\lambda_{1},\lambda_{2}]} $$.
où A est un coefficient constant pour un instrument donné, qu’on appelle coefficient d’étalonnage absolu.
- la luminance ne dépend plus des caractéristiques instrumentales.
Dans cette équation, tous les éléments sont des caractéristiques de l’instrument, exceptée la luminance spectrale équivalente, qui elle est indépendante des caractéristiques de l’instrument. Les mesures obtenues sont donc proportionnelles à la luminance du pixel observé, à un facteur(S.G.t) près qui ne dépend que de l’instrument. Les concepteurs de l’instrument vont donc chercher à faire en sorte que S.G.t soit :
- le plus grand possible, pour augmenter la sensibilité et le rapport signal sur bruit
- le plus uniforme possible d’un pixel à l’autre, pour éviter de faire apparaître dans l’image des variations qui ne proviendraient pas de la scène observée.
La réflectance
Pour les longueurs d’ondes inférieures à 3 µm, la luminance des surfaces terrestres provient essentiellement de la réflexion par la terre de l’éclairement solaire (à l’exception de quelques sources lumineuses très intenses : projecteurs orientés vers le satellite, coulées de lave (dans le moyen infra rouge)…). Afin de s’abstraire de l’éclairement solaire, qui dépend de la distance entre la terre et le soleil (variable avec la saison), l’introduction d’une nouvelle unité est nécessaire : il s’agit de la réflectance (c’est la dernière grandeur à définir, nous sommes au bout du calvaire). La réflectance spectrale se définit par :
$$\rho(\lambda)=\frac{\pi.L(\lambda)}{Es(\lambda,t).cos(\theta_{s})}\label{eq:def reflectance spectrale}$$
On définit par ailleurs de la même manière la réflectance équivalente :
$$\rho{}_{eq\,[\lambda_{1},\lambda_{2}]}=\frac{\pi.L{}_{eq\,[\lambda_{1},\lambda_{2}]}}{Es{}_{eq\,[\lambda_{1},\lambda_{2}]}(t).cos(\theta_{s})}$$
La formulation ci-dessus peut surprendre au premier abord, on aurait pu s’attendre à une formule beaucoup plus simple, la réflectance étant égale à la luminance divisée par l’éclairement. La formule adoptée pour définir la réflectance provient de considérations géométriques. Le flux reçu sur une surface dépend de son orientation par rapport à la source lumineuse. Si la surface est perpendiculaire aux rayons lumineux, le flux est maximum, alors que si elle est parallèle, il devient nul. Ceci explique la présence du cos(θs). Le facteur de normalisation π fait en sorte que la réflectance soit égale à 1 si la surface réfléchit vers le ciel la totalité de l’éclairement incident. Pour nous en convaincre, il suffit de calculer l’intégrale de la luminance réfléchie dans toutes les directions par une surface dont la réflectance est égale à 1 ( sans oublier que pour intégrer sur la sphère, il faut utiliser le facteur $$sin \theta_{s} d\theta_{s} d\phi$$ et non pas seulement $$ d\theta_{s} d\phi$$.
$$\intop_{\theta=0}^{\frac{\pi}{2}}\intop_{\phi=0}^{2\pi}Lsin\theta_{s}d\theta_{s}d\varphi=\intop_{\theta=0}^{\frac{\pi}{2}}\intop_{\phi=0}^{2\pi}\frac{Es.cos\theta_{s}}{\pi}sin\theta_{s}d\theta_{s}d\varphi=\frac{E_{s}}{\pi}\intop_{\theta=0}^{\frac{\pi}{2}}\intop_{\phi=0}^{2\pi}\cdot cos\theta_{s}.sin\theta_{s}.d\theta_{s}d\varphi=E_{s}$$
puisque :$$\intop_{\theta=0}^{\frac{\pi}{2}}\intop_{\phi=0}^{2\pi} cos\theta_{s}sin\theta_{s}d\theta_{s}d\varphi$$
$$=2\pi.\intop_{\theta=0}^{\frac{\pi}{2}}sin\theta_{s}d(sin\theta_{s})=2\pi\frac{sin^{2}\frac{\pi}{2}}{2}=\pi$$
La réflectance est une caractéristique de la surface et ne dépend ni de l’instrument qui l’observe ni de l’éclairement reçu. Cette réflectance dépend cependant de l’angle sous lequel la surface est éclairée et observée et aussi, bien sûr, de la longueur d’onde. On entend parfois parler de l’albédo spectral qui est la moyenne de la réflectance dans toutes les directions, ou de l’albédo, qui est la moyenne de l’albédo spectral sur tout le spectre.
$$a(\lambda)=\frac{1}{\pi}\intop_{\theta=0}^{\pi}\intop_{\phi=0}^{2\pi}\rho(\lambda).d\theta_{s}d\varphi$$
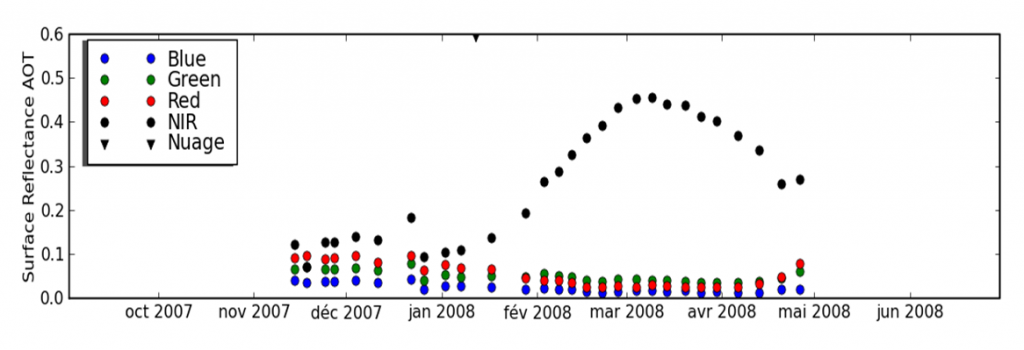
Cette fois, nous sommes au bout de nos peines, et nous avons démontré que les mesures de nos satellites sont proportionnelles à une grandeur caractéristique de la surface, la réflectance. C’est en réflectance que les données Sentinel-2, ou LANDSAT sont exprimées, même s’il nous a fallu discuter avec les tenants de la luminance. La réflectance présente en effet de nombreux avantages :
- La réflectance est une caractéristique de la surface, elle ne dépend que de la surface et des angles d’éclairement et d’observation (cf les effets directionnels)
- Ses valeurs sont en général comprises entre zéro et un (même si des valeurs supérieures à 1 peuvent être observées, c’est assez rare). Ces valeurs sont faciles à mémoriser, contrairement aux valeurs de luminances, qui varient d’une bande à l’autre en fonction de l’éclairement solaire
- Il est possible de comparer les réflectances d’une bande spectrale à l’autre.
- Il est possible de comparer directement les réflectances mesurées en hiver et en été, sans avoir à prendre en compte la variation de l’élévation solaire.

Excellente explication
Olivier, merci pour tes fiches très instructives. J’ai toutefois une question, tu dis « C’est en réflectance que les données Sentinel-2, ou LANDSAT sont exprimées, même s’il nous a fallu discuter avec les tenants de la luminance ». Il faut comprendre que tu parles des données fournies au niveau 2, c’est bien ça ? Les tenants de la luminance voulaient plutôt une calibration des comptes numériques par les gains de calibrations des images et les autres une tranformation de plus pour aboutir à la réflectance TOA ? As-tu les courbes en luminance de la dernière figure de cette fiche ? Tu nous annonce qu’elles sont beaucoup moins intéressantes. Merci.
Bonjour Dominique,\nle débat sur l’unité à utiliser pour les produits de Niveau 1 opposait les tenants de la luminance et de la réflectance. Pour la luminance, l’argument principal est qu’il s’agit d’une unité du S.I. Mais les avantages de la réflectance sont nombreux :\n- même ordre de grandeur dans chaque bande spectrale, compris entre 0 et 1 généralement, et donc facile à mémoriser. Une surface blanche a une réflectance constante et élevée.\n- la luminance est une propriété de la surface, contrairement à la luminance, qui dépend de l’éclairement solaire.\n- les satellites sont étalonnés en réflectance, la connaissance de la réflectance est plus précise que la connaissance de la luminance.\n\nTu as raison, je devrais afficher la même courbe en luminance, on verrait des variations saisonnières qui ne correspondent pas à un signal de surface. Mais je n’ai plus les données d’origine sous la main pour faire ce tracé…\n\nCordialement,\nOlivier\n- .
très bien fait, mais pour le peu physicien comme moi, je pense qu’il faut bien insister sur les unités de chaque grandeur, et donc faire l’équation de dimension pour expliciter par exemple que la reflectance est sans dimension (sans unités).
Merci Olivier , c’est assez physique ..J’ai un bon tuto pour Landsat https://landsat.usgs.gov/sites/default/files/documents/LSDS-1656_Landsat_Level-1_Product_Collection_Definition.pdfJ'utilise les images landsat de la collection LTP1? que pense tu de ce format, les corrections semblent suffisantes pour toi ? Merci
Bonjour Michel,\nOn ne se refait pas ;)\nOui, il faut utiliser les nouvelles collections Landsat, Mais ce produit ne corrige pas les effets atmosphériques. \nJe ne sais pas où se situe ta zone d’intérêt, mais depuis peu, Theia corrige aussi les données Landsat sur la France, et les fournit sur la même grille que Sentinel-2 (https:///theia.cnes.fr). Sinon, le produit de niveau 2 Surface Reflectance de l’USGS est de bonne qualité: https://landsat.usgs.gov/landsat-surface-reflectance-data-products\nCordialement,\nOlivier
quel est le nom du paramèrte radiométrique qui corespond a l’unité energétique rapportée a la surface de la source de lumière.
Bonjour,
la puissance lumineuse (le flux) divisée par une surface, porte deux noms, l’éclairement si la surface en question est le récepteur, ou l’exitance ou emittance, si la surface est la source. Mais c’est vrai que seul l’observateur change entre les deux quantités, d’un point de vue physique, c’est la même quantité, mesurée en W/m2
Olivier
Bonjour et merci beaucoup pour votre mémo technique.
Une coquille je pense dans le texte : « La luminance est une unité très utilisée en télédétection, puisqu’elle combine plusieurs avantages […] ».
Voici ma proposition de correction => « La luminance (dont l’unité est le W.m-2.sr-1) est une grandeur physique très utilisée en télédétection, puisqu’elle combine plusieurs avantages […] «
Effectivement, je corrige. Merci pour le retour.
bonjour,
Pourriez vous aussi faire une fiche pour la résolution radiométrique sur le domaine du radar(diffusiomètre)?